Los vectores de dirección del primer plano, los (3,2,4) y (1,0,2) junto con
los del segundo, los (4,3,5) y (1,1,1) , forman un sistema cuyo rango es:
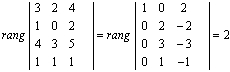
Luego los planos son paralelos
La ecuación del primer plano que pasa por el punto (4,-3,5) y tiene como
vectores directores (3,2,4) y (1,0,2) es:
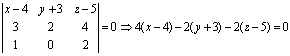
4x-16-2y-6-2z+10
= 0 =>
4x-2y-2z-12 = 0 =>
2x - y - z -12 = 0
n1 = ( 2, -1, -1)
La ecuación del segundo plano que pasa por el punto (4,-3,5) y tiene como
vectores directores (3,2,4) y (1,0,2) es:

-2x+2+y-3+z-2 = 0
=>
2x - y - z + 3 = 0 =>
n2 = ( 2, -1
,-1)
Son planos paralelos pues sus vectores de dirección normal
son iguales
Si esto último no lo ves, ¡ haz el producto
vectorial ! entre:
n1 = ( 2, -1, -1) y n2 = ( 2, -1 ,-1)
y si da 0 es que el ángulo que forman es cero, por lo que tendrán la misma
dirección (paralelos)
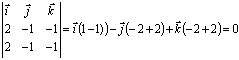
Como cabía esperar